Análisis geoestadístico con ArcGIS parte 1. Estadística descriptiva
Antes de abordar en firme, el modulo de geoestadistica que viene con ArcGIS, es necesario recordar algunos conceptos de estadística, en particular de estadística descriptiva, que son necesarios para realizar un análisis geoestadístico con el software.
La estadística descriptiva, se dedica a los métodos de recolección, descripción, visualización y resumen de datos originados a partir de los fenómenos de estudio. Para analizar los datos usualmente se construyen las tablas de frecuencias y se utilizan: la media, mediana, moda, desviación estándar, la varianza, coeficiente de curtosis, coeficiente de sesgo, coeficiente de variación, cuartiles, deciles y percentiles. Estos parámetros se agrupan en varias categorías conocidas como medidas de tendencia central, medidas de dispersión y medidas de forma.
Tablas de Frecuencias
Una forma de presentar ordenadamente un grupo de observaciones, es a través de tablas de distribución de frecuencias. Para construir una tabla de frecuencia se deben ordenar los datos de menor a mayor e incluir los siguientes parámetros.
| Frecuencia Absoluta (ni) | Es el número de datos que están en un mismo intervalo. |
| Frecuencia Relativa (fi) | Es la frecuencia absoluta dividida por el número total de datos. |
| Frecuencia Absoluta Acumulada (Ni) | Es la suma de las frecuencias absolutas de todos los valores inferiores o iguales al valor considerado. La última frecuencia absoluta acumulada es igual al número de casos. |
| Frecuencia Relativa Acumulada (Fi) | Es el resultado de dividir cada frecuencia absoluta acumulada por el número total de datos. |
| Numero de clases | Indica el número de intervalos en que se agruparan los datos. |
| Amplitud de la clase o intervalo | Se obtiene al dividir por dos, la diferencia del valor máximo y mínimo de los datos. |
| Marca de clase | Es el promedio de la suma del límite superior e inferior de cada intervalo o clase. |
En el caso de datos agrupados se deberán determinar el número de intervalos, la amplitud de los mismos y la marca de clase, de la siguiente forma:

Distribución normal
Una distribución de probabilidad sigue una distribución normal, cuando la representación gráfica de su función de densidad es una curva positiva continua, simétrica respecto a la media, de máximo en la media, y que tiene 2 puntos de inflexión situados a ambos lados de la media y a distancia igual a la desviación estándar, es decir de la forma:
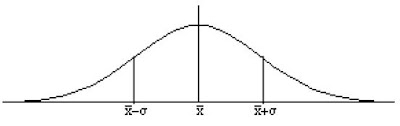
Propiedades.
- Tiene una única moda, que coincide con su media y su mediana.
- La curva normal es asintótica al eje de abscisas.
- Es simétrica con respecto a su media. Según esto, para este tipo de variables existe una probabilidad de un 50% de observar un dato mayor que la media, y un 50% de observar un dato menor.
- Cuanto mayor sea la desviación estándar, más se dispersarán los datos en torno a la media y la curva será más plana. Un valor pequeño de este parámetro indica, por tanto, una gran probabilidad de obtener datos cercanos al valor medio de la distribución.
- El coeficiente de sesgo es igual a cero (0).
- La curtosis es igual a cero (0).
Para la aplicación de los métodos geoestadísticos es necesario verificar la función de probabilidad del conjunto de datos se aproximen a un comportamiento normal, esto lo veremos más adelante en el análisis exploratorio de los datos.
Con el fin de que este sea un ejemplo práctico para abordar el análisis geoestadistico con ArcGIS, ilustraremos todo los conceptos con un ejemplo a partir de datos de monitoreo de niveles piezométricos de agua subterránea que se presentan en la tabla siguiente. Para ello se seguirán los siguientes pasos.
- Organizar los datos de menor a mayor.
- Calcular la tabla de frecuencia.
- Realizar el histograma de frecuencias.
- Calcular los parámetros geoestadístico.
Paso 1. Organizar los datos de menor a mayor
| Pozo | X | Y | Nivel Pz (msnm) |
Pozo | X | Y | Nivel Pz (msnm) |
| 1 | 1.038.638 | 1.368.620 | 2,0 | 28 | 1.044.694 | 1.371.405 | 6,00 |
| 2 | .034.835 | 1.344.198 | 2,1 | 29 | 1.041.841 | 1.363.397 | 6,1 |
| 3 | 1.039.637 | 1.368.963 | 2,2 | 30 | 1.040.838 | 1.356.677 | 8,0 |
| 4 | 1.039.628 | 1.368.960 | 2,2 | 31 | 1.044.135 | 1.364.301 | 8,07 |
| 5 | 1.042.236 | 1.377.584 | 2,44 | 32 | 1.046.740 | 1.377.526 | 8,08 |
| 6 | 1.039.030 | 1.370.440 | 2,49 | 33 | 1.046.626 | 1.374.772 | 9,02 |
| 7 | .036.835 | 1.354.454 | 2,9 | 34 | 1.042.604 | 1.360.903 | 9,21 |
| 8 | 1.043.217 | 1.357.777 | 2,99 | 35 | 1.039.466 | 1.348.279 | 10,1 |
| 9 | 1.040.082 | 1.373.095 | 3,2 | 36 | 1.041.429 | 1.333.870 | 10,3 |
| 10 | 1.039.392 | 1.374.231 | 3,3 | 37 | 1.045.207 | 1.363.183 | 10,8 |
| 11 | 1.040.434 | 1.368.119 | 3,33 | 38 | 1.044.733 | 1.360.337 | 11,5 |
| 12 | 1.039.720 | 1.368.500 | 3,35 | 39 | 1.048.893 | 1.374.744 | 11,82 |
| 13 | 1.042.060 | 1.376.470 | 3,43 | 40 | 1.040.383 | 1.355.006 | 12,2 |
| 14 | 1.041.545 | 1.369.212 | 3,7 | 41 | 1.042.263 | 1.354.636 | 12,3 |
| 15 | 1.042.045 | 1.371.752 | 3,8 | 42 | 1.039.411 | 1.336.953 | 12,8 |
| 16 | 1.040.269 | 1.377.908 | 3,97 | 43 | 1.048.342 | 1.369.941 | 14,62 |
| 17 | 1.040.731 | 1.371.643 | 4,0 | 44 | 1.046.214 | 1.355.644 | 14,9 |
| 18 | 1.042.360 | 1.376.070 | 4,29 | 45 | 1.044.935 | 1.336.931 | 16,6 |
| 19 | 1.040.390 | 1.376.776 | 4,5 | 46 | 1.041.256 | 1.339.628 | 18,16 |
| 20 | 1.035.335 | 1.356.941 | 4,5 | 47 | 1.048.313 | 1.360.466 | 19,14 |
| 21 | 1.047.035 | 1.371.548 | 4,62 | 48 | 1.044.224 | 1.348.328 | 24,1 |
| 22 | 1.042.020 | 1.370.310 | 4,66 | 49 | 1.044.765 | 1.341.254 | 24,2 |
| 23 | 1.033.716 | 1.352.675 | 5,0 | 50 | 1.046.735 | 1.356.327 | 25,57 |
| 24 | 1.042.570 | 1.377.470 | 5,10 | 51 | 1.045.454 | 1.346.959 | 27,15 |
| 25 | 1.035.564 | 1.343.433 | 5,2 | 52 | 1.050.523 | 1.361.111 | 30,08 |
| 26 | 1.042.520 | 1.368.530 | 5,38 | 53 | 1.052.106 | 1.361.728 | 35,32 |
| 27 | 1.042.932 | 1.368.255 | 5,87 |
Paso 2. Calcular la tabla de frecuencia.

Luego la tabla de frecuencias queda como la siguiente
| # | Intervalo | Marca de clase | Frecuencia absoluta |
Frecuencia absoluta acumulada |
Frecuencia relativa |
Frecuencia relativa acumulada |
| 1 | 2,0076 - 6,1776 | 4,0926 | 29 | 29 | 0,55 | 0,55 |
| 2 | 6,1776 - 10,3476 | 8,2626 | 7 | 36 | 0,13 | 0,68 |
| 3 | 10,3476 - 14,5176 | 12,4326 | 6 | 42 | 0,11 | 0,79 |
| 4 | 14,5176 - 18,6876 | 16,6026 | 4 | 46 | 0,08 | 0,87 |
| 5 | 18,6876 - 22,8576 | 20,7726 | 1 | 47 | 0,02 | 0,89 |
| 6 | 22,8576 - 27,0276 | 24,9426 | 4 | 51 | 0,08 | 0,96 |
| 7 | 27,0276 - 31,1976 | 29,1126 | 1 | 52 | 0,02 | 0,98 |
| 8 | 31,1976 - 35,3676 | 33,2826 | 1 | 53 | 0,02 | 1,00 |
Paso 3. Realizar el histograma de frecuencias.
A partir de la tabla anterior se construye el histograma de frecuencias, el cual nos da una idea del comportamiento de los datos. Como primer acercamiento, se observa que los datos están dispersos, sesgados y la moda, la media y la mediana son diferentes, por tanto los datos no obedecen a una distribución normal.
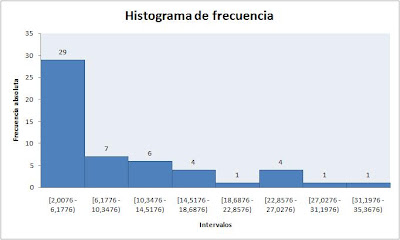
Paso 4. Calcular los parámetros geoestadístico
a. Medidas de tendencia central
Intentan identificar el dato más representativo de la distribución del conjunto. Son las siguientes.
Media. Se le suele llamar promedio, se define como la suma de los valores de todas las observaciones divididas por el número total de datos. Se denota con µ o X.
En su cálculo intervienen todos los datos, por lo tanto, se ven influenciados por la variación de cualquiera de ellos. En particular, es sensible a los valores extremos, pues estos producen grandes modificaciones.

Para los datos agrupados del ejemplo, tenemos lo siguiente….
| # | Intervalo | Marca de clase (Xi) | Frecuencia absoluta | Producto |
| 1 | 2,0076 - 6,1776 | 4,0926 | 29 | 118,685 |
| 2 | 6,1776 - 10,3476 | 8,2626 | 7 | 57,838 |
| 3 | 10,3476 - 14,5176 | 12,4326 | 6 | 74,596 |
| 4 | 14,5176 - 18,6876 | 16,6026 | 4 | 66,410 |
| 5 | 18,6876 - 22,8576 | 20,7726 | 1 | 20,773 |
| 6 | 22,8576 - 27,0276 | 24,9426 | 4 | 99,770 |
| 7 | 27,0276 - 31,1976 | 29,1126 | 1 | 29,113 |
| 8 | 31,1976 - 35,3676 | 33,2826 | 1 | 33,283 |
| Suma | 500,468 | |||
| Media (suma/53) | 9,443 |
Para los datos no agrupados
Pozo | NP | Pozo | NP | |
1 | 2,0076 |
| 28 | 6,0000 |
2 | 2,1313 |
| 29 | 6,1496 |
3 | 2,2000 |
| 30 | 8,0054 |
4 | 2,2100 |
| 31 | 8,0724 |
5 | 2,4449 |
| 32 | 8,0827 |
6 | 2,4946 |
| 33 | 9,0188 |
7 | 2,8554 |
| 34 | 9,2078 |
8 | 2,9876 |
| 35 | 10,1156 |
9 | 3,2347 |
| 36 | 10,2553 |
10 | 3,2930 |
| 37 | 10,8373 |
11 | 3,3317 |
| 38 | 11,5066 |
12 | 3,3506 |
| 39 | 11,8241 |
13 | 3,4291 |
| 40 | 12,2268 |
14 | 3,6896 |
| 41 | 12,3280 |
15 | 3,7990 |
| 42 | 12,8004 |
16 | 3,9651 |
| 43 | 14,6244 |
17 | 3,9980 |
| 44 | 14,9301 |
18 | 4,2921 |
| 45 | 16,6351 |
19 | 4,4900 |
| 46 | 18,1630 |
20 | 4,5286 |
| 47 | 19,1410 |
21 | 4,6227 |
| 48 | 24,0632 |
22 | 4,6637 |
| 49 | 24,2354 |
23 | 5,0499 |
| 50 | 25,5698 |
24 | 5,1009 |
| 51 | 27,1534 |
25 | 5,2438 |
| 52 | 30,0800 |
26 | 5,3826 |
| 53 | 35,3188 |
27 | 5,8690 |
|
| |
Suma | 497,0104 | |||
Media (suma/53) | 9,3776 | |||
Mediana. Es el valor de la serie de datos que deja la mitad de las observaciones por debajo de ella y la otra mitad por encima, es decir, divide al conjunto de datos en dos partes iguales y se denota por Me.
Dado que sólo depende del orden de los datos, tiene la ventaja de que no es sensible a los valores extremos.
En datos agrupados se calcula de la siguiente forma.
- Calcular: n/2
- La mediana será el valor de la variable cuya frecuencia absoluta acumulada primero iguale o supere a N/2. Este será el intervalo en el que se encuentra la mediana.
- Aplicar la formula sustituyendo los valores correspondientes.

Para datos agrupados, tenemos lo siguiente….
Se calcula n/2 = 53/2 = 26.5, se busca este valor en la columna de la frecuencia acumulada de la tabla de frecuencia. Si no se encuentra, tomamos el valor siguiente, el cual es 29, por lo cual el intervalo donde se encuentra la moda es (2.0076 – 6.1776].
Fi=29
Fi-1=8
Li= 2.0076
a= 4.17
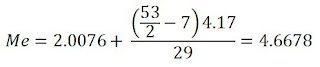
Para datos no agrupados, tenemos lo siguiente….
Como el número de datos de la muestra es impar e igual a 53, la mediana es el dato que ocupa el puesto 27(divide la muestra en dos partes iguales), el cual es: Me= 5.8690
Moda. Es el dato que más veces se repite, es decir, aquel dato o rango que presenta mayor frecuencia absoluta. Puede haber más de una moda en una distribución. Se denota por Mo.

Para datos agrupados, tenemos lo siguiente….
De los datos agrupados en la tabla de frecuencia, se observa que la mayor frecuencia absoluta es 29, por lo tanto el intervalo donde está la moda es (2.0076 – 6.1776].
Li=2.0076
a=4.17
d2=29-7 = 22
d1=29-0 = 29

b. Medidas de dispersión
Las medidas de dispersión indican la mayor o menor concentración de los datos con respecto a las medidas de centralización. Nos dan una idea sobre la homogeneidad o que tan agrupado están los datos.
Desviación estándar. Indica cuánto tienden a alejarse los valores puntuales de la media. Se suele representar por una S. Una desviación estándar grande indica que los puntos están lejos de la media, y una desviación pequeña indica que los datos están agrupados cerca de la media.

Para datos agrupados, tenemos lo siguiente….
| # | Intervalo | Marca de clase (Xi) | Frecuencia absoluta | (Xi-X)²*fi |
| 1 | 2,0076 - 6,1776 | 4,0926 | 29 | 830,111 |
| 2 | 6,1776 - 10,3476 | 8,2626 | 7 | 9,750 |
| 3 | 10,3476 - 14,5176 | 12,4326 | 6 | 53,634 |
| 4 | 14,5176 - 18,6876 | 16,6026 | 4 | 205,052 |
| 5 | 18,6876 - 22,8576 | 20,7726 | 1 | 128,365 |
| 6 | 22,8576 - 27,0276 | 24,9426 | 4 | 960,977 |
| 7 | 27,0276 - 31,1976 | 29,1126 | 1 | 386,901 |
| 8 | 31,1976 - 35,3676 | 33,2826 | 1 | 568,337 |
| Suma | 3143,12 | |||
| n-1 | 52 | |||
| S | 7,774 |
Para datos no agrupados….
Pozo | NP | (Xi-X)² |
| Pozo | NP | (Xi-X)² |
1 | 2,0076 | 54,3169 |
| 28 | 6,000 | 11,4082 |
2 | 2,1 | 52,5089 |
| 29 | 6,150 | 10,4200 |
3 | 2,2 | 51,5179 |
| 30 | 8,005 | 1,8829 |
4 | 2,2 | 51,3745 |
| 31 | 8,072 | 1,7035 |
5 | 2,44 | 48,0623 |
| 32 | 8,083 | 1,6768 |
6 | 2,49 | 47,3757 |
| 33 | 9,019 | 0,1287 |
7 | 2,9 | 42,5391 |
| 34 | 9,208 | 0,0288 |
8 | 2,99 | 40,8321 |
| 35 | 10,116 | 0,5446 |
9 | 3,2 | 37,7352 |
| 36 | 10,255 | 0,7704 |
10 | 3,3 | 37,0224 |
| 37 | 10,837 | 2,1307 |
11 | 3,33 | 36,5529 |
| 38 | 11,507 | 4,5326 |
12 | 3,35 | 36,3247 |
| 39 | 11,824 | 5,9854 |
13 | 3,43 | 35,3852 |
| 40 | 12,227 | 8,1179 |
14 | 3,7 | 32,3533 |
| 41 | 12,328 | 8,7049 |
15 | 3,8 | 31,1208 |
| 42 | 12,800 | 11,7156 |
16 | 3,97 | 29,2952 |
| 43 | 14,624 | 27,5289 |
17 | 4,0 | 28,9401 |
| 44 | 14,930 | 30,8303 |
18 | 4,29 | 25,8628 |
| 45 | 16,635 | 52,6713 |
19 | 4,5 | 23,8886 |
| 46 | 18,163 | 77,1833 |
20 | 4,5 | 23,5128 |
| 47 | 19,141 | 95,3240 |
21 | 4,62 | 22,6091 |
| 48 | 24,063 | 215,6668 |
22 | 4,66 | 22,2209 |
| 49 | 24,235 | 220,7542 |
23 | 5,0 | 18,7290 |
| 50 | 25,570 | 262,1873 |
24 | 5,10 | 18,2902 |
| 51 | 27,153 | 315,9791 |
25 | 5,2 | 17,0883 |
| 52 | 30,080 | 428,5894 |
26 | 5,38 | 15,9600 |
| 53 | 35,319 | 672,9459 |
27 | 5,87 | 12,3103 |
|
|
|
|
suma | 3.363,14 | |||||
n-1 | 52 | |||||
S | 8,042 | |||||
Varianza. Describe la variabilidad de la distribución. Es la medida de la desviación o dispersión de la distribución. Se calcula mediante la ecuación.

Para datos agrupados, tenemos lo siguiente….
S² = 7.774² = 60.44
Para datos no agrupados, tenemos lo siguiente….
S² = 8.042² = 64.675
Coeficiente de variación. Mide la representatividad de la media. Valores extremos del mismo nos llevarán a concluir que la media no es representativa, es decir, existirán valores entre las observaciones que se separan significativamente de las demás.

Para datos agrupados, tenemos lo siguiente….
C.V = 7.74/9.443*100 = 82%
Para datos no agrupados, tenemos lo siguiente….
C.V = 8.042/9.3776*100 = 85.8%
c. Medidas de forma
Miden el grado de deformación respecto a una curva patrón (distribución normal).
Coeficiente de curtosis. Mide el grado de aplastamiento o apuntamiento de la gráfica de la distribución de la variable estadística. Datos concentrados respecto a la media (desviación estándar pequeña) dará una grafica alargada; si los datos están dispersos la gráfica será achatada o aplastada.

Nota: El valor calculado a través de la herramienta Geostatistical Analyst de ArcGIS no le resta 3 como aparece en la ecuación anterior.

Para datos no agrupados tenemos, lo siguiente:
Pozo | NP | (Xi-X)4 |
| Pozo | NP | (Xi-X)4 |
1 | 2,0076 | 2.950,3256 |
| 28 | 6,000 | 130,1466 |
2 | 2,1 | 2.757,1808 |
| 29 | 6,150 | 108,5761 |
3 | 2,2 | 2.654,0983 |
| 30 | 8,005 | 3,5454 |
4 | 2,2 | 2.639,3382 |
| 31 | 8,072 | 2,9021 |
5 | 2,44 | 2.309,9875 |
| 32 | 8,083 | 2,8115 |
6 | 2,49 | 2.244,4559 |
| 33 | 9,019 | 0,0166 |
7 | 2,9 | 1.809,5744 |
| 34 | 9,208 | 0,0008 |
8 | 2,99 | 1.667,2604 |
| 35 | 10,116 | 0,2966 |
9 | 3,2 | 1.423,9469 |
| 36 | 10,255 | 0,5935 |
10 | 3,3 | 1.370,6549 |
| 37 | 10,837 | 4,5400 |
11 | 3,33 | 1.336,1150 |
| 38 | 11,507 | 20,5448 |
12 | 3,35 | 1.319,4859 |
| 39 | 11,824 | 35,8246 |
13 | 3,43 | 1.252,1157 |
| 40 | 12,227 | 65,9010 |
14 | 3,7 | 1.046,7389 |
| 41 | 12,328 | 75,7746 |
15 | 3,8 | 968,5028 |
| 42 | 12,800 | 137,2543 |
16 | 3,97 | 858,2062 |
| 43 | 14,624 | 757,8409 |
17 | 4,0 | 837,5292 |
| 44 | 14,930 | 950,5047 |
18 | 4,29 | 668,8854 |
| 45 | 16,635 | 2.774,2665 |
19 | 4,5 | 570,6668 |
| 46 | 18,163 | 5.957,2546 |
20 | 4,5 | 552,8518 |
| 47 | 19,141 | 9.086,6611 |
21 | 4,62 | 511,1702 |
| 48 | 24,063 | 46.512,1891 |
22 | 4,66 | 493,7663 |
| 49 | 24,235 | 48.732,4260 |
23 | 5,0 | 350,7750 |
| 50 | 25,570 | 68.742,2017 |
24 | 5,10 | 334,5301 |
| 51 | 27,153 | 99.842,7699 |
25 | 5,2 | 292,0101 |
| 52 | 30,080 | 183.688,8444 |
26 | 5,38 | 254,7224 |
| 53 | 35,319 | 452.856,1270 |
27 | 5,87 | 151,5428 |
|
|
|
|
suma | 954.116,25 | |||||
n-1 | 52 | |||||
S4 | 4182,95 | |||||
K | 1,38 | |||||
Coeficiente de sesgo o asimetría. Evalúa el grado de distorsión o inclinación que adopta la distribución de los datos respecto a su valor promedio tomado como centro de gravedad. El coeficiente de simetría de Pearson es:

Si CS = 0, la distribución es simétrica, en ese caso las desviaciones a la derecha y a la izquierda de la media se compensan.
Si CS < 0, la distribución es asimétrica negativa. La mayoría de las observaciones están a la derecha de la proyección de la media.
Si CS > 0 la distribución es asimétrica positiva. La mayoría de las observaciones están a la izquierda de la proyección de la media.

Para datos no agrupados tenemos, lo siguiente:
Pozo | NP | (Xi-X)3 |
| Pozo | NP | (Xi-X)3 |
1 | 2,0076 | -400,3156 |
| 28 | 6,000 | -38,5323 |
2 | 2,1 | -380,4950 |
| 29 | 6,150 | -33,6357 |
3 | 2,2 | -369,7752 |
| 30 | 8,005 | -2,5838 |
4 | 2,2 | -368,2318 |
| 31 | 8,072 | -2,2235 |
5 | 2,44 | -333,2017 |
| 32 | 8,083 | -2,1712 |
6 | 2,49 | -326,0869 |
| 33 | 9,019 | -0,0462 |
7 | 2,9 | -277,4485 |
| 34 | 9,208 | -0,0049 |
8 | 2,99 | -260,9171 |
| 35 | 10,116 | 0,4019 |
9 | 3,2 | -231,8037 |
| 36 | 10,255 | 0,6761 |
10 | 3,3 | -225,2662 |
| 37 | 10,837 | 3,1102 |
11 | 3,33 | -220,9952 |
| 38 | 11,507 | 9,6500 |
12 | 3,35 | -218,9291 |
| 39 | 11,824 | 14,6432 |
13 | 3,43 | -210,4909 |
| 40 | 12,227 | 23,1296 |
14 | 3,7 | -184,0258 |
| 41 | 12,328 | 25,6828 |
15 | 3,8 | -173,6104 |
| 42 | 12,800 | 40,1000 |
16 | 3,97 | -158,5600 |
| 43 | 14,624 | 144,4387 |
17 | 4,0 | -155,6861 |
| 44 | 14,930 | 171,1850 |
18 | 4,29 | -131,5267 |
| 45 | 16,635 | 382,2620 |
19 | 4,5 | -116,7581 |
| 46 | 18,163 | 678,0858 |
20 | 4,5 | -114,0136 |
| 47 | 19,141 | 930,6861 |
21 | 4,62 | -107,5039 |
| 48 | 24,063 | 3.167,1971 |
22 | 4,66 | -104,7469 |
| 49 | 24,235 | 3.279,9221 |
23 | 5,0 | -81,0534 |
| 50 | 25,570 | 4.245,3899 |
24 | 5,10 | -78,2215 |
| 51 | 27,153 | 5.616,7807 |
25 | 5,2 | -70,6396 |
| 52 | 30,080 | 8.872,8285 |
26 | 5,38 | -63,7603 |
| 53 | 35,319 | 17.457,0231 |
27 | 5,87 | -43,1918 |
|
|
|
|
suma | 39.576,74 | |||||
n-1 | 52 | |||||
S3 | 520,13 | |||||
Sesgo | 1,46 | |||||
A continuación se muestran los resultados obtenidos a través de las ecuaciones de datos agrupados y no agrupados, también se incluyen los resultados arrojados por la herramienta Geostatistical Analyst (la cual se verá más adelante). Se observa que los resultados obtenidos tanto por las ecuaciones aplicadas a datos no agrupados y los obtenidos por la herramienta Geostatistical Analyst son similares.
| Parámetro | Datos agrupados | Datos no agrupados | Módulo Geostatistical analyst de ArcGIS |
Observaciones |
| Media | 9.443 | 9.3776 | 9.3776 | |
| Mediana | 4.6678 | 5.869 | 5.869 | |
| Moda | 4.378 | |||
| Desviación estándar | 7.74 | 8.0421 | 8.0421 | |
| Varianza | 60.44 | 64.675 | 64.675 | |
| Coeficiente de Variación | 82% | 85.8% | 85.75% | |
| Curtosis | 1.38 | 1.4709 | A la curtosis que calcula ArcGIS se le debe restar 3 |
|
| Sesgo o asimetría | 1.46 | 1.4773 |
En el artículo Análisis geoestadístico con ArcGIS parte 2. Análisis exploratorio de los datos veremos el análisis exploratorio de los datos para después abordar el tutorial de la herramienta Geostatistical Analyst.